I am currently working on making my own whiteboard program using Dear ImGui, and one of the features I had to implement was the ability to select objects on the whiteboard. Since ImGui does not offer click detections for custom shapes, I had to implement my own selection detection algorithm. With the help of some vector math and the Internet, it was actually quite straightforward.

Framing the Problem

Whether an object should be selected can be framed as asking how close a mouse click is to an object. If the distance is below a threshold, then we can consider the object to be selected.

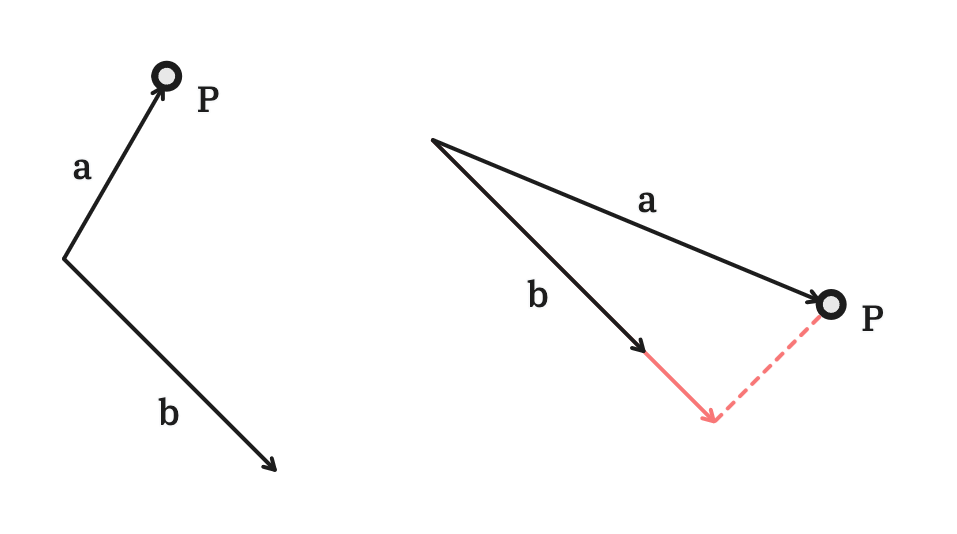
Let’s reframe this question again in math. Consider a line (segment) $\textbf{b}$ with two points, $v_1$ and $v_2$, and point $P$, where the mouse click happened. The problem is to find a point on $\textbf{b}$ that is closest to $P$. Intuitively, that point can be found by drawing a perpendicular line from $P$ to $\textbf{b}$, and the intersection point will be the closest point on $\textbf{b}$ to $P$. The distance between the two points then becomes the closest distance between $P$ and $\textbf{b}$. Below is an illustration of the problem:

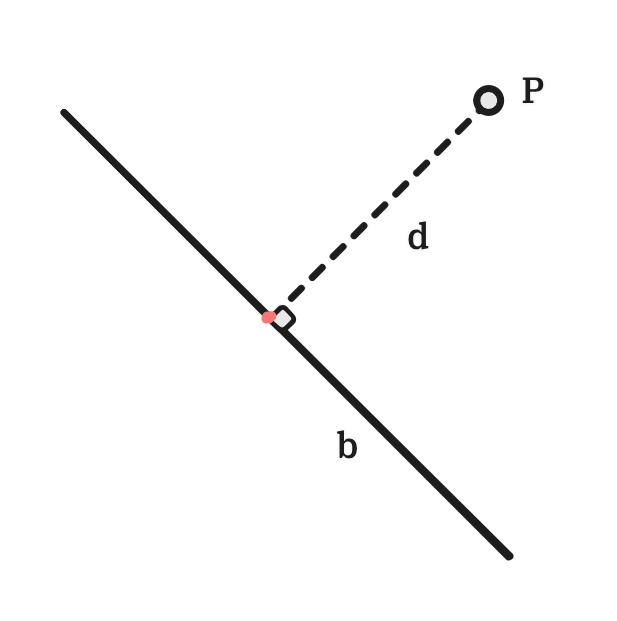
where:

• $P$ is the point where the mouse click occurred;
• $\textbf{b}$ is the line that can be selected; and
• $d$ is the shortest distance between $P$ and $\textbf{b}$.

Applying Vector Math

Notice how the letter $\textbf{b}$ is bolded. This means that the line is treated as a vector. Now, we introduce another vector $\textbf{a}$ from the beginning of $\textbf{b}$ to $P$. Observe that the projection of $\textbf{a}$ onto $\textbf{b}$ $proj_{\textbf{b}}\textbf{a}$ points to the shortest point on $b$ from $P$.

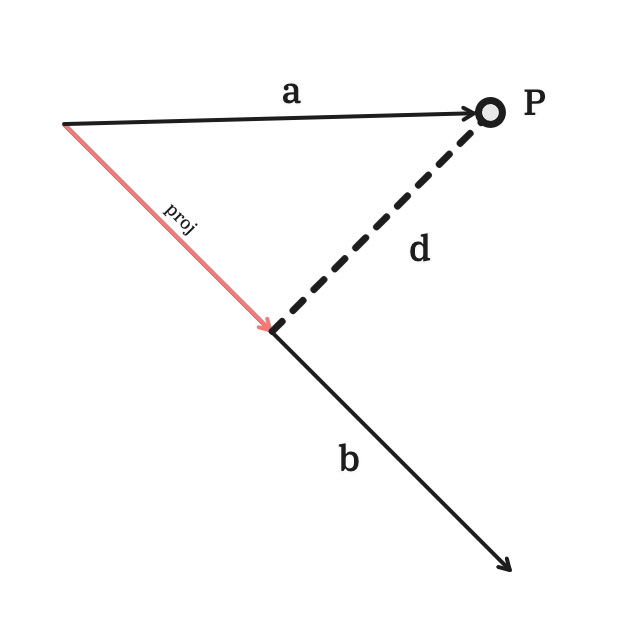
The projection is written as:

$$proj_{\textbf{b}}\textbf{a} = \frac{\textbf{a}\cdot\textbf{b}}{||\textbf{b}||} \hat{\textbf{b}}$$

where

• $||\textbf{b}||$ is the magnitude of $\textbf{b}$
• $\hat{\textbf{b}}$ is the unit vector of $\textbf{b}$

Recall that the magnitude of a vector $\textbf{a}$ is defined as:

$$||\textbf{a}|| = \sqrt{\sum_{i=1}^{n}x_i^2}$$

and its unit vector as:

$$\hat{\textbf{a}} = \frac{\textbf{a}}{||\textbf{a}||}$$

for any finite n-dimensional vector $\textbf{a} \in \mathbb{R}^n$.

Substituting into the projection formula, we get

$$proj_{\textbf{b}}\textbf{a} = \frac{\textbf{a}\cdot\textbf{b}}{\textbf{b}\cdot\textbf{b}}\textbf{b}$$

Finding $\textbf{a}$ and $\textbf{b}$

To find $\textbf{a}$, we treat $v_1$ and $P$ as two vectors:

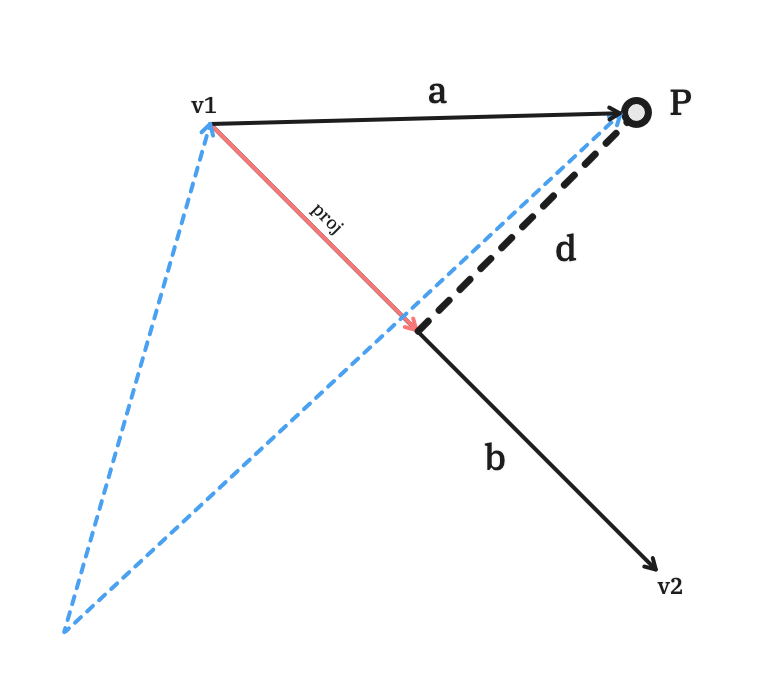
Then, we subtract $\textbf{v}_1$ from $\textbf{P}$ using vector subtraction:

$$\textbf{a} = \textbf{P} - \textbf{v}_1$$

$\textbf{b}$ can be found in a similar fashion.

Finding the Intersection Point

Once the projection vector is found, we add it to $\textbf{v}_1$ to obtain the coordinates of the intersection point:

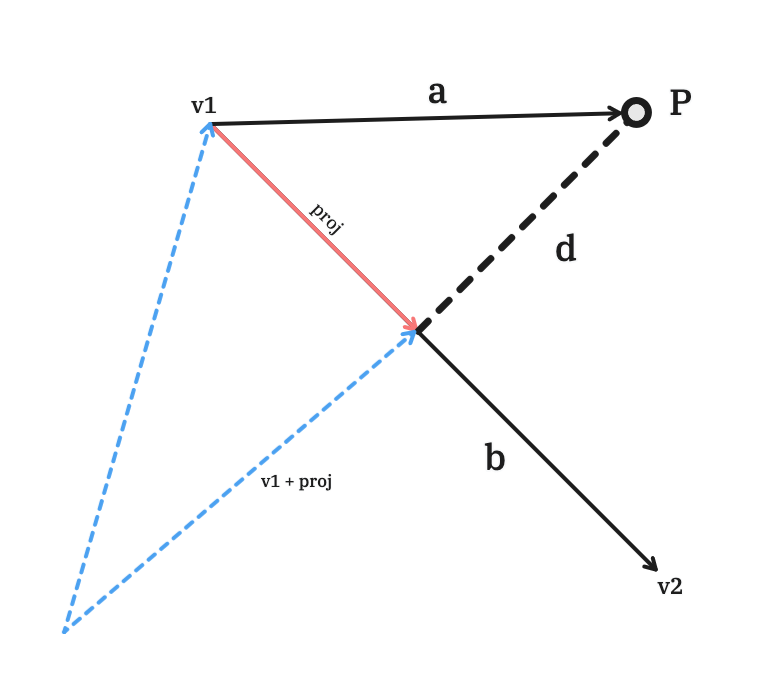
Computing the Shortest Distance

Finally, to find the shortest distance between $P$ and $\textbf{b}$, we now have two choices:

• Find the euclidean distance between $P$ and the intersection point
• Perform vector subtraction between the two points, then find its magnitude.

In either case, we have successfully found the shortest distance between a point and a line segment!

Special Cases

There are two special cases that we have not considered:

1. The projection of the point falls outside of $\textbf{b}$ to the left of it
2. The projection of the point falls outside of $\textbf{b}$ to the right of it

In the first case, the dot product $\textbf{a} \cdot \textbf{b}$ is less than zero. Therefore, if we find that the dot product is less than zero, we know that the closest point from $P$ to $\textbf{b}$ is the starting point of $\textbf{b}$.

In the second case, the projection of $\textbf{a}$ onto $\textbf{b}$ is longer than $\textbf{b}$. We can write this relation as:

$$\begin{align} ||proj_{\textbf{b}}\textbf{a}|| &> ||\textbf{b}|| \nonumber \\ \frac{\textbf{a}\cdot\textbf{b}}{||\textbf{b}||} &> ||\textbf{b}|| \nonumber \\ \textbf{a}\cdot\textbf{b} &> ||\textbf{b}||^2 \nonumber\\ \textbf{a}\cdot\textbf{b} &> \textbf{b}\cdot\textbf{b} \nonumber\\ \end{align}$$

Therefore, when $\textbf{b}\cdot\textbf{b}$ is greater than $\textbf{a}\cdot\textbf{b}$, we know that we are in the second case, and we can infer that the end point of $\textbf{b}$ is the closest to $P$.

Implementation Note

At the final step of finding the distance between a point and the intersection point, a square root is involved using either method. Since we only care about whether the distance meets a threshold and not the actual number, we can skip the square root calculation and compare it with the square of the threshold we want. For example, if we want the threshold to be 5px for an object to be considered selected, we compare the computation with $5^2 = 25$.